甘肃民族师范学院2020年普通高职(专科)升本科考试水利水电工程专业考试大纲
一、考试目的
通过对《高等数学》的学习,考察学生基础知识、基本技能和思维能力、运算能力、以及分析问题和解决问题的能力。
通过对《材料力学》的学习,考察学生掌握杆件的强度、刚度和稳定性的基本理论的程度;着重观察其基本概念和基本方法熟练程度,学生应该具有良好的计算能力,一定的分析问题的能力和实验能力。
二、考试内容
(一)高等数学
第一章 函数、极限与连续
1.知识点:函数的概念与基本特性;数列、函数极限;极限的运算法则;两个重要极限;无穷小的概念与阶的比较;函数的连续性和间断点;闭区间上连续函数的性质。
2.考核要求:理解函数的概念,了解函数的奇偶性、单调性、周期性、有界性。了解反函数的概念;理解复合函数的概念。理解初等函数的概念。会建立简单实际问题的函数关系。理解数列极限、函数极限的概念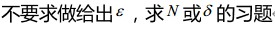 ;了解极限性质(唯一性、有界性、保号性)和极限的两个存在准则(夹逼准则和单调有界准则)。掌握函数极限的运算法则;熟练掌握极限计算方法。掌握两个重要极限,并会用两个重要极限求极限。了解无穷小、无穷大、高阶无穷小、等价无穷小的概念,会用等价无穷小求极限。理解函数连续的概念;了解函数间断点的概念,会判别间断点的类型(第一类可去、跳跃间断点与第二类间断点)。了解初等函数的连续性;了解闭区间上连续函数的性质,会用性质证明一些简单结论。
;了解极限性质(唯一性、有界性、保号性)和极限的两个存在准则(夹逼准则和单调有界准则)。掌握函数极限的运算法则;熟练掌握极限计算方法。掌握两个重要极限,并会用两个重要极限求极限。了解无穷小、无穷大、高阶无穷小、等价无穷小的概念,会用等价无穷小求极限。理解函数连续的概念;了解函数间断点的概念,会判别间断点的类型(第一类可去、跳跃间断点与第二类间断点)。了解初等函数的连续性;了解闭区间上连续函数的性质,会用性质证明一些简单结论。
第二章 导数与微分
1.知识点:导数概念及求导法则;隐函数与参数方程所确定函数的导数;高阶导数;微分的概念与运算法则。
2.考核要求:理解导数的概念及几何意义,了解函数可导与连续的关系,会求平面曲线的切、法线方程;掌握导数的四则运算法则和复合函数的求导法则;掌握基本初等函数的求导公式,会熟练求函数的导数。掌握隐函数与参数方程所确定函数的求导方法(一阶);掌握取对数求导法。了解高阶导数的概念,掌握初等函数的一阶、二阶导数的求法。会求简单函数的n阶导数。理解微分的概念,了解微分的运算法则和一阶微分形式不变性,会求函数的微分。
第三章 中值定理与导数应用
1.知识点:罗尔中值定理、拉格朗日中值定理;洛必达法则;函数单调性与极值、曲线凹凸性与拐点。
2.考核要求:理解罗尔中值定理、拉格朗日中值定理(对定理的分析证明不作要求);会用中值定理证明一些简单的结论。掌握用洛必达法则求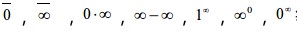 等不定式极限的方法。理解函数极值概念,掌握用导数判定函数的单调性和求函数极值的方法;会利用函数单调性证明不等式;会求较简单的最大值和最小值的应用问题。会用导数判断曲线的凹凸性,会求曲线的拐点。
等不定式极限的方法。理解函数极值概念,掌握用导数判定函数的单调性和求函数极值的方法;会利用函数单调性证明不等式;会求较简单的最大值和最小值的应用问题。会用导数判断曲线的凹凸性,会求曲线的拐点。
第四章 不定积分
1.知识点:原函数与不定积分概念,不定积分换元法,不定积分分部积分法。
2.考核要求:理解原函数与不定积分的概念和性质。掌握不定积分的基本公式、换元积分法和分部积分法(淡化特殊积分技巧的训练,对于有理函数积分的一般方法不作要求,对于一些简单有理函数可作为两类积分法的例题作适当训练)。
第五章 定积分及其应用
1.知识点:定积分的概念和性质,积分变上限函数,牛顿-莱布尼兹公式,定积分的换元积分法和分部积分法,无穷区间上的广义积分;定积分的应用——求平面图形的面积与旋转体体积。
2.考核要求:理解定积分的概念,了解定积分的性质和积分中值定理。理解积分变上限函数的概念和性质,掌握牛顿-莱布尼兹公式,能正确运用该公式计算定积分。掌握定积分的换元法和分部积分法。了解定积分的元素法,会计算平面图形的面积和旋转体的体积。理解无穷区间上广义积分的概念,并会求无穷区间上的广义积分。
第六章 微分方程
1.知识点:微分方程的基本概念,可分离变量微分方程与齐次方程,一阶线性微分方程,二阶常系数线性微分方程。
2.考核要求:了解微分方程以及微分方程的阶、解、通解、初始条件和特解等概念。掌握可分离变量微分方程的解法。会解齐次方程(可转化为可分离变量微分方程的方法)。了解一阶线性微分方程的常数变异法,掌握一阶线性微分方程的解法。了解二阶线性微分方程解的结构,掌握二阶常系数齐次线性微分方程求解方法。会用待定系数法求自由项为简单函数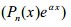 的二阶常系数非齐次线性微分方程的特解方法。
的二阶常系数非齐次线性微分方程的特解方法。
第七章 空间解析几何向量代数
1.知识点:空间直角坐标系、向量及其运算、空间平面及其方程、空间直线及其方程、二次曲面。
2.考核要求:理解空间直角坐标系的概念,理解向量的概念及其表示;会求空间两点的距离。掌握向量的运算(线性运算、数量积、向量积),了解两个向量垂直、平行的条件。会求平面方程、直线方程。掌握平面与平面、直线与平面、直线与直线平行与垂直的条件,会求点到平面的距离。了解曲面方程的概念,了解常用二次曲面的方程及其图形。
第八章 多元函数微分学
1.知识点:二元函数概念、二元函数极限、连续,偏导数、全微分、多元函数的求导法则,隐函数求导公式,多元函数微分学的几何应用,多元函数极值。
2.考核要求:理解二元函数的概念,了解多元函数的概念。了解二元函数的极限和连续的概念,会求一些简单二元函数的极限。理解二元函数偏导数与全微分的概念,了解全微分存在的必要条件与充分条件。掌握多元函数偏导数与全微分的计算方法。掌握多元复合函数一阶偏导数的求法。会求解隐函数的一阶偏导数。了解曲线的切线与法平面、曲面的切平面与法线等概念,并会求它们的方程;理解二元函数极值与条件极值的概念,会求简单的二元函数的极值。了解拉格朗日乘数法,会求一些比较简单的最大值与最小值的应用问题。
第九章 多元函数积分学
1.知识点:二重积分与三重积分的概念与性质、二重积分与三重积分的计算。曲线积分、格林公式。
2.考核要求:理解二重积分的概念与性质。掌握二重积分的计算方法(直角坐标、极坐标)。了解三重积分的概念。会计算简单的三重积分(直角坐标、柱面坐标)。理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系,掌握两类曲线积分的计算方法。掌握格林公式,掌握平面曲线积分与路径无关的条件及应用。
第十章 无穷级数
1.知识点:常数项级数的概念和性质,常数项级数敛散性的判别;幂级数的概念和性质,函数的幂级数展开。
2.考核要求:理解无穷级数以及收敛、发散、和的概念,了解无穷级数的基本性质及收敛的必要条件。掌握几何级数和
-级数的收敛性。掌握正项级数的比值审敛法,了解正项级数的比较审敛法。掌握交错级数的莱布尼兹定理,理解绝对收敛与条件收敛的概念,会判断交错级数的绝对收敛与条件收敛。理解幂级数的概念,掌握幂级数收敛半径、收敛区间、收敛域及和函数的求法。会利用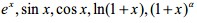 的麦克劳林展开式将一些简单函数展开成幂级数。
的麦克劳林展开式将一些简单函数展开成幂级数。
(二)材料力学
第一章 绪论及基本概念
1.知识点:构件强度、刚度和稳定性的概念;本课程的主要任务;可变形固体的概念和基本假设;基本变形杆件的受力和变形特征。
2.考核要求:明确构件强度、刚度和稳定性,可变形固体的概念,课程的主要任务;理解材料力学的基本假设;了解基本变形杆件的受力和变形特征。
第二章 轴向拉伸与压缩
1.知识点:内力与截面法,轴力、轴力图;拉(压)杆横截面上的应力分布及其计算公式;线应变,胡克定律,弹性模量,泊松比;拉(压)杆变形的计算公式与应用;低碳钢拉伸时的应力—应变曲线与应力特征值,强度指标与塑性指标;铸铁拉伸破坏与压缩破坏行为的比较;安全系数,工作应力,许用应力,危险应力;强度条件,三类强度问题;拉(压)杆的超静定问题;应力集中的概念,圣维南原理。
2.考核要求:理解求解内力的截面法,掌握轴力图的绘制方法;明确胡克定律,弹性模量,泊松比等概念,熟练掌握拉(压)杆变形的计算;掌握材料的强度指标和塑性指标及其测试方法;明确安全系数,工作应力,许用应力等概念,熟练掌握拉压杆强度条件及相关的计算;掌握简单拉(压)超静定问题的求解方法;了解应力集中的概念。
第三章 轴向拉伸与压缩
1.知识点:剪切和挤压的概念;剪切和挤压的实用强度计算;剪应力与剪应变,剪切胡克定律。
2.考核要求:了解剪切与挤压的概念;理解剪应变的概念剪切胡克定律;掌握剪切和挤压的实用强度计算。
第四章 圆轴扭转
1.知识点:扭转的概念及外力偶矩计算;扭转时横截面上的内力—扭矩;圆轴扭转时横截面上的应力;圆轴扭转强度条件及应用;圆轴扭转变形及刚度条件。
2.考核要求:了解扭转的概念,掌握外力偶矩和扭矩的计算;掌握圆轴扭转应力和变形的计算;掌握圆轴扭转强度条件及其应用;了解圆轴扭转刚度条件及其应用。
第五章 弯曲应力和弯曲变形
1.知识点:平面弯曲的概念及梁的计算简图;剪力和弯矩的概念,剪力图和弯矩图的绘制方法;弯曲正应力公式,截面惯性矩的计算;常见截面梁的最大剪应力公式;梁的正应力强度条件、剪应力强度条件及其应用;挠度与转角的概念,求解梁变形的积分法;常见简单梁的挠度公式,梁的刚度校核;提高梁强度和刚度的措施。
2.考核要求:了解弯曲的概念和梁横截面上的应力的分布特点;熟练掌握梁剪力图与弯矩图的绘制方法;掌握常见梁截面惯性矩的计算;熟练掌握梁正应力强度条件及其应用;掌握用积分法求解梁的挠度和转角;了解梁刚度校核和提高梁强度和刚度措施。
第六章 应力状态与强度理论
1.知识点:应力状态的概念;平面应力状态的主应力、最大剪应力公式;强度理论。
2.考核要求:了解应力状态的概念;掌握平面应力状态的主应力、最大剪应力的计算;了解强度理论及其应用。
第七章 组合变形构件的强度
1.知识点:组合变形构件强度计算的原理;拉(压)与+弯曲组合变形构件的强度计算;偏心压缩与截面核心的概念。
2.考核要求:了解斜弯曲、偏心压缩、截面核心的概念;熟练掌握拉(压)与弯曲组合变形构件的强度计算。
第八章 压杆稳定
1.知识点:压杆稳定与临界力的概念;确定临界力的欧拉公式;柔度的概念,压杆的临界应力,临界应力总图;压杆的稳定性校核;提高压杆稳定性的措施。
2.考核要求:明确压杆稳定、临界力、柔度和临界应力总图的概念;熟练掌握常见细长压杆临界力的计算;了解稳定性校核方法和提高压杆稳定性的措施。
三、试题难易程度
较容易题 约30%
中等难度题 约50%
较难题 约20%
四、说明
试卷满分为200分,《高等数学》和《材料力学》各为100分。考试时间为120分钟。
五、参考书目
1.《高等数学》(第七版),同济大学数学系,高等教育出版社,2014年07月。
2.《材料力学Ⅰ》(第五版),孙训方,高等教育出版社,2009年07月。
内容摘要:优思途甘肃专升本网按往年惯例,在第一时间对已发布的院校招生简章进行了转载,以下就对各院校2026年招生简章的发布情况做汇总整理。对于已发布的院校,可以直接点击下方表格中的“已发布”进行浏览...
TAGS:甘肃专升本 招生简章